Fibonacci Indicators
Fibonacci Numbers
Fibonacci numbers are named after Leonardo Fibonacci, a twelfth century Italian mathematician, who discovered the unique properties of a particular number sequence; apparently from studying the dimensions of the Great Pyramid at Gizeh in Egypt.
| Fibonacci numbers |
| 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, etc. |
| Each number in the sequence is the sum of the previous two numbers: 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, and so on.... |
The Golden Ratio
As we progress along the sequence, the ratio of each number to its preceding number approaches closer and closer to the golden ratio: approximately 1.618. The golden ratio, often represented by the Greek letter Φ (Phi), is calculated as:
( 1 + √ 5 ) / 2
Each number is also approximately 0.618 of its successor. This reciprocal number, known as φ (phi), is calculated as:
( √ 5 - 1 ) / 2
Where √ 5 is the square root of 5.
| Fibonacci Golden Ratio and its Reciprocal | |||
| Each number divided by its predecessor approaches 1.618 | Each number divided by its successor approaches 0.618 | ||
| 1/1 | 1.0 | 1/1 | 1.0 |
| 2/1 | 2.0 | 1/2 | 0.5 |
| 3/2 | 1.5 | 2/3 | 0.666... |
| 5/3 | 1.666... | 3/5 | 0.6 |
| 8/5 | 1.6 | 5/8 | 0.625 |
| 13/8 | 1.625 | 8/13 | 0.61538... |
| 21/13 | 1.61538... | 13/21 | 0.61905... |
| 34/21 | 1.61905... | 21/34 | 0.61765... |
| 55/34 | 1.61765... | 34/55 | 0.61818... |
| 89/55 | 1.61818... | 55/89 | 0.61798... |
Fibonacci Numbers in Nature
Fibonacci numbers occur throughout nature:
- the arrangement of petals in most flowers
- the arrangement of leaves on most plants
- sea-shell spirals
- the arrangement of seeds on sunflowers, pine cones and many other plant species.
While the Fibonacci number sequence may be prevalent in nature, it is not a universal law. There are many exceptions.
Fibonacci Ratios
Four ratios are normally plotted:
- 0.618 (or 61.8 per cent), the reciprocal of the golden ratio, is the most important;
- 0.50 (or 50 per cent) - the second number divided by the third (1 divided by 2);
- 0.382 (or 38.2 per cent) - the reciprocal of the golden ratio squared (i.e. 89 / 233);
- 0.236 (or 23.6 per cent) - the reciprocal of the golden ratio cubed (i.e. 55 / 233).
Fibonacci and Stocks
Fibonacci ratios regularly occur in stock market cycles and in the determination of support and resistance levels. Some traders attach almost mystical significance to them, but I have yet to find any statistical support for this.
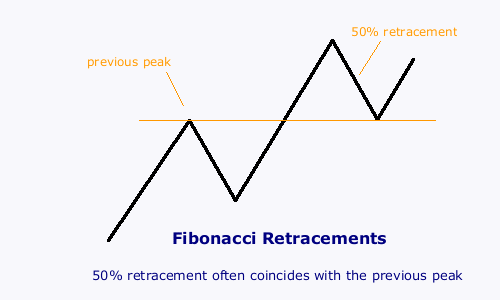
The weakest of the Fibonacci ratios is 0.50. In fact some maintain that 0.50 is not really a Fibonacci ratio at all because it has no connection to the golden ratio. Nevertheless, it is probably the most prevalent: the first line of support in a rally is the previous peak -- which often equates to a 50% retracement.
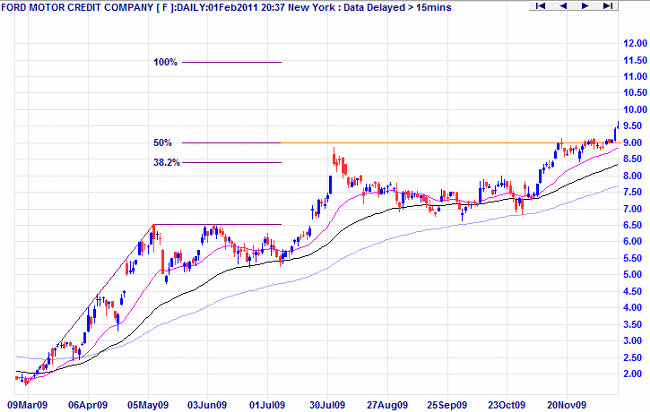
What are Fibonacci Extension Levels?
Extensions are used to project likely targets for the next leg of an up- or down-trend. Percentage extension levels, based on significant Fibonacci numbers, are plotted as horizontal lines above/below the previous trend move.
For more details on how to setup click here.
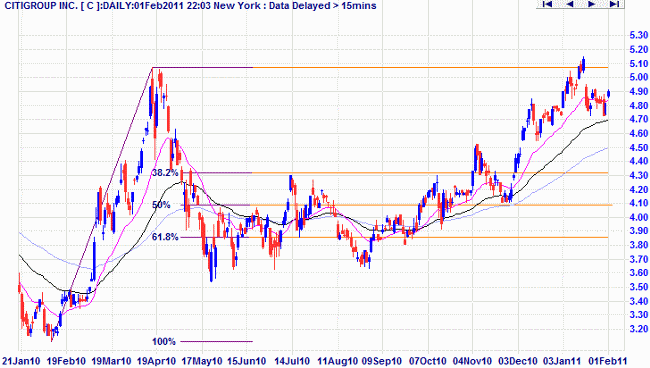
What are Fibonacci Retracement Levels?
Retracements are used to estimate likely reversal points during an up- or down-trend. Percentage retracement levels, based on significant Fibonacci numbers, are plotted as horizontal lines against the latest trend move.
For more details on how to setup click here.