The 2 Percent Rule
The 2% Rule is a basic tenet of risk management (I prefer the terms "risk management" or "capital preservation" as they are more descriptive than "money management"). Even if the odds are stacked in your favor, it is not advisable to risk a large portion of your capital on a single trade.
Larry Hite, in Jack Schwager's Market Wizards (1989), mentions two lessons learned from a friend:
- Never bet your lifestyle -- never risk a large chunk of your capital on a single trade; and
- Always know what the worst possible outcome is.
Hite goes on describe his 1 percent rule which he applies to a wide range of markets. This has since been adapted by short-term equity traders as the 2 Percent Rule:
NEVER RISK MORE THAN 2 PERCENT OF YOUR CAPITAL ON ANY ONE STOCK.
This means that a run of 10 consecutive losses would only consume 20% of your capital. It does not mean that you need to trade 50 different stocks! If you use stop losses, such as ATR Trailing Stops, your capital at risk is normally far less than the purchase price of the stock.
How to Apply the 2 Percent Rule
- Calculate 2 percent of your trading capital: your Capital at Risk
- Deduct brokerage on the buy and sell to arrive at your Maximum Permissible Risk
- Calculate your Risk per Share:
Deduct your stop-loss from the buy price and add a provision for slippage (not all stops are executed at the actual limit). For a short trade, the procedure is reversed: deduct the buy price from the stop-loss before adding slippage. - The Maximum Number of Shares is then calculated by dividing your Maximum Permissible Risk by the Risk per Share.
Example: 2% Rule
Imagine that your total share trading capital is $20,000 and your brokerage costs are fixed at $50 per trade.
- Your Capital at Risk is: $20,000 * 2 percent = $400 per trade.
- Deduct brokerage, on the buy and sell, and your Maximum Permissible Risk is: $400 - (2 * $50) = $300.
- Calculate your Risk per Share:
If a stock is priced at $10.00 and you want to place a stop-loss at $9.50, then your risk is 50 cents per share.
Add slippage of say 25 cents and your Risk per Share increases to 75 cents per share. - The Maximum Number of Shares that you can buy is therefore:
$300 / $0.75 = 400 shares (at a cost of $4000)
Quick Test
Your capital is $20,000 and brokerage is $20 per trade.
A share is trading at $10.00 per share and you will place your stop loss at $9.25.
How many shares can you purchase? Apply the 2 percent rule.
Hint: Remember to allow for brokerage, on the buy and sell, and slippage (of say 25 cents/share).
Adapt the 2% Rule to your Trading Style
Not all traders face the same success rate (or reliability as Van Tharp calls it). Short-term traders usually achieve higher success rates, while long-term traders generally expect greater risk-reward ratios.
Success Rate (Reliability)
Your success rate is the number of winning trades expressed as a percentage of your total number of trades:
Success rate = winning trades / (winning trades + losing trades) * 100%
Risk-Reward Ratios
Your risk-reward ratio is your expected gain compared to your capital at risk (it should really be called the reward/risk ratio because that is the way it is normally expressed). If your average gain (after deducting brokerage) on winning trades is $1000 and you have consistently risked $400 per trade (as in the earlier 2 percent rule example), then your risk-reward ratio would be 2.5 to 1 (i.e. $1000 / $400).
Risk-Reward ratio = average gain on winning trades / average capital at risk
Confidence Levels
If we have three traders:
| Trader: | A | B | C |
|---|---|---|---|
| Time frame: | Short-term | Medium | Long-term |
| Success Rate: | 75% | 50% | 25% |
| Risk-Reward Ratio: | 1.0 | 3.0 | 10.0 |
Trader A
Trades short-term and averages 125% profit over all his trades.
| Winning trades: | 75% * 1 | 0.75 |
|---|---|---|
| Less: Losing Trades | 25% * 1 | -0.25 |
| Average Profit | .50 | |
| As a percentage of capital at risk | 50% |
Trader B
Trades medium-term and averages 200% profit over all his trades.
| Winning trades: | 50% * 3 | 1.50 |
|---|---|---|
| Less: Losing Trades | 50% * 1 | -0.50 |
| Average Profit | 1.00 | |
| As a percentage of capital at risk | 100% |
Trader C
Trades long-term and averages 325% profit over all her trades.
| Winning trades: | 25% * 10 | 2.50 |
|---|---|---|
| Less: Losing Trades | 75% * 1 | -0.75 |
| Average Profit | 1.75 | |
| As a percentage of capital at risk | 175% |
This does not necessarily mean that Trader C is more profitable than A. Trader A (short-term) is likely to make many more trades than Trader C. You could have the following situation:
| Trader: | A | B | C |
|---|---|---|---|
| Time frame: | Short-term | Medium | Long-term |
| Average Profit/Trade | 50% | 100% | 175% |
| Number of Trades/Year | 300 | 100 | 40 |
| Times Return on Capital at Risk | 150 | 100 | 70 |
| Capital at Risk | 2% | 2% | 2% |
| Annual % Return on Capital | 300% | 200% | 140% |
Relative Risk
We now calculate the relative risk that each trader has of a 20% draw-down. Use the binomial probability calculator at http://vassarstats.net/textbook/ch5apx.html:
| Trader | A | B | C |
|---|---|---|---|
| Success Rate | 75% | 50% | 25% |
| Probability of 10 straight losses | 0.0001% | 0.1% | 5.6% |
Obviously, the higher your success rate, the greater the percentage that you can risk on each trade.
Bear in mind that, with a higher risk-reward ratio, Trader C only needs one win in 10 trades to break even; while Trader A would need five wins. However, if we compare breakeven points, it is still clear that lower success rates are more likely to suffer from draw-downs.
| Trader | A | B | C |
|---|---|---|---|
| Number of wins (out of 10 trades) required to break even | 5 | 2.5 | 1 |
| Normal Success Rate | 75% | 50% | 25% |
| Probability of making a net loss in 10 trades | 2.0% | 5.5% | 5.6% |
Low Success Rates
Although your trading system may be profitable, if it has a low success rate it will be susceptible to large draw-downs. Consider using a lower percentage of capital at risk: not more than 1% capital at risk per trade if your expected success rate is below 50%.
Trading in the Real World
In real life, we do not trade with a perfect binomial distribution as in the above example:
- gains are not all equal;
- some losses are bigger than others — stop losses occasionally fail when prices gap up/down;
- probabilities vary; and
- outcomes influence each other — when stocks fall, they tend to fall together.
Covariance
The biggest flaw in most risk management systems is that stock movements influence each other. Individual trades are not independent. Markets march in unison and individual stocks follow. Of course there are mavericks — stocks that rise in a bear market or collapse in the middle of a bull market — but they are a handful. The majority follow like a flock of sheep.
Thomas Dorsey in Point & Figure Charting gives an example of the risks affecting a typical stock:
|
Market risk Sector risk Stock risk |
66% 24% 10% |
The risk of the market moving against you is clearly the biggest single risk factor. How do we protect against this?
Protecting your Capital from a String of Losses
The 2 percent rule alone will not protect you if you are holding a large number of banking stocks during an asset bubble; insurance stocks during a natural disaster; or technology stocks during the Dotcom boom. We need a quick rule of thumb to measure our exposure to a particular industry or market.
Independent Sectors
Limit your exposure to specific industry sectors. Not all sectors are created equal, however. Industry groups in the (ICB or GICS) Raw Materials sector have fairly low correlation, and can be treated as separate sectors, while industry groups in most other sectors should be treated as a single unit.
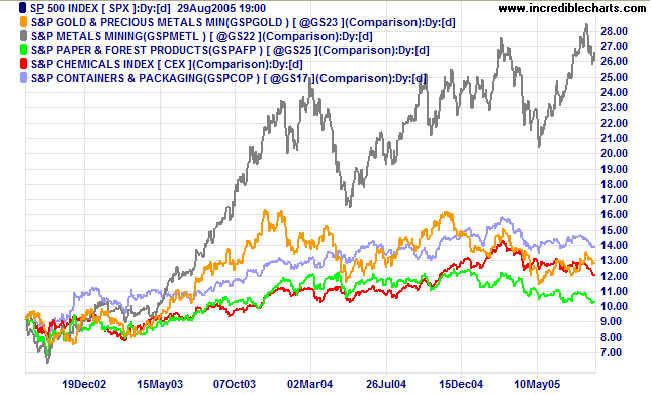
We can see from the above chart that Chemicals and Containers & Packaging tend to move in unison and should possibly be treated as one industry sector, but other indexes shown are sufficiently independent to be treated separately.
Sector Risk
As a rule of thumb, limit your exposure to any one industry sector to 3 stocks (e.g. 6% capital at risk if you are using the 2 percent rule).
This does not mean that you are limited to holding 3 stocks in any one sector. You may buy a fourth stock when one of your initial 3 trades is no longer at risk (when you have moved the stop up above your breakeven point on the trade); and a fifth when you have covered your risk on another trade; and so on.
Just be careful not to move your stops up too quickly. In your haste you may be stopped out too early -- before the trend gets under way.
I also suggest that you tighten your stops across all positions in a sector if protective stops are triggered on 3 straight trades in that sector (within a reasonable time period). By protective stops I mean a trailing stop designed to exit your position if the trend changes (e.g. a close below a long-term MA). A reasonable time period may vary from a few days for short-term trades to several weeks for long-term trades.
Market Risk
You can limit our market risk in a similar fashion.
Limit your Total Capital at Risk in the market to between 5 and 10 stocks (e.g. 10% to 20% capital at risk if you are using the 2 percent rule). Adjust this percentage to suit your own risk profile. Also, the shorter your time frame and the higher your Success Rate, the greater the percentage that you can comfortably risk.
It is also advisable to tighten your stops across all positions if protective stops are triggered on 5 consecutive trades within a reasonable time period. Protective stops do not have to be the original stops set on a trade. You may make an overall profit on the trade, but the stop should indicate a trend change.
2% Rule Money Management Summary
A general rule for equity markets is to never risk more than 2 percent of your capital on any one stock. This rule may not be suitable for long-term traders who enjoy higher risk-reward ratios but lower success rates. Do not risk more than 1% of your capital on each trade if the expected success rate is below 50%.
The 2% rule should also not be applied in isolation. Your biggest risk is market risk, when most stocks move in unison. To protect against this, limit your capital at risk in any sector, and also your capital at risk in the entire market, at any one time.

Author: Colin Twiggs is a former investment banker with over 30 years experience in financial markets. He co-founded Incredible Charts and writes the popular Trading Diary newsletter.
Colin also writes The Patient Investor newsletter which focuses on the global economic outlook and key macro trends.
In addition, he founded PVT Capital (AFSL No. 546090) which offers investment strategy and advice to wholesale clients.
